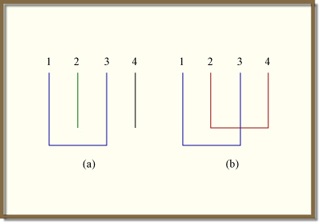
The power of infinite random matrix theory comes from being able to systematically identify and work with non-crossing partitions (as depicted on the left). The figure on the right depicts a crossing partition which becomes important when trying to understand the higher order terms which infinite random matrix theory cannot predict. (Figure by Prof. Alan Edleman.)
Instructor(s)
Prof. Moe Win
Prof. Alan Edelman
MIT Course Number
18.338J / 16.394J
As Taught In
Fall 2004
Level
Graduate
Course Description
Course Features
Course Description
In this course on the mathematics of infinite random matrices, students will learn about the tools such as the Stieltjes transform and Free Probability used to characterize infinite random matrices.


