|
Home | 18.013A | Chapter 19 |
||
|
|
||
We know how to anti-differentiate a function of the form ![]() for
any a and b. This will allow us to find the anti-derivative of a rational function
for
any a and b. This will allow us to find the anti-derivative of a rational function ![]() if we can reduce it to a sum of terms of that form and possibly a polynomial
instead.
if we can reduce it to a sum of terms of that form and possibly a polynomial
instead.
If p(x) has a higher degree than q(x) we can extract a quotient polynomial s(x) by a process akin to long division called synthetic division.
We may then be left with a remainder polynomial r(x). We know how to anti-differentiate
s(x) so the task of anti-differentiating ![]() reduces
to anti-differentiating
reduces
to anti-differentiating ![]() where the numerator has lower degree than the denominator.
where the numerator has lower degree than the denominator.
Suppose now that we can factor q into factors like (x-a) or (x-b)3 or ((x-d)2+ c2)m.
The wonderful fact is that the expression ![]() can
be separated into terms each of which has the form
can
be separated into terms each of which has the form ![]() or
or
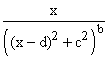 for some a's, d's and c's and integer values of b, each of which can be anti-differentiated.
for some a's, d's and c's and integer values of b, each of which can be anti-differentiated.
And here is a procedure for separating it.
Suppose the denominator q can be factored into (x-b)kt(x) such that t(b) is not 0.
And suppose we find the first k terms of the Taylor series expansion
of ![]() about x = b
about x = b
![]()
Then the terms in ![]() that involve inverse powers of (x-b) are given as follows:
that involve inverse powers of (x-b) are given as follows:
If k = 1 there is only one term, ![]()
For k = 2 we have ![]() where A is as before while B is
where A is as before while B is 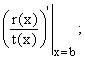 and so on.
and so on.
There are similar rules for quadratic factors.
The process of separating the denominator q in this manner is called "the method of partial fractions".
We review the various methods again in Section 27.1 and some integrals to practice on are given in Section 27.3. We apologize for the redundancy.
|
|